DP: Max Subset Sum No Adjacent Problem bp.1

In this first blog post about dynamic programming problems, we are going to solve an easy problem called Max Subset Sum No Adjacent. I encourage you to read the prompt and take time 10-15 minutes to think about how would you solve this problem, then read the solution.

Prompt:

Write a function that takes in an array of positive integers and returns the maximum sum of non-adjacent elements in the array. If the input array is empty the function should return 0.

Sample Input:

array = [75, 105, 120, 75, 90, 135]

Sample Output:

330 // 75 + 120 +135

Explanation:

Did you take the time to think about the solution? I hope you did 😅

Using dynamic programming to solve this problem means that we are going to solve smaller problems and use these smaller solutions to build up our final solution.

For our problem here, we are going to build an array of the same length as our input array. In this new array, we are going to store the greatest sum we can generate with no adjacent numbers up until and including the index at which we are storing that sum, and without necessarily using the number at this index.

But let's have an array with smaller numbers for simplicity:

First, we construct a new array of the same length as our input array and call it maxSums.

@ index 0: we have the number 7, so the greatest number we can generate with no adjacent numbers here is just 7. Easy enough 🙂

@ index 1: we have the number 10, and we know that we can't add 7 and 10 because they are adjacent elements in the array. So we are going to take the greatest of the two numbers, which is 10.

@ index 2: we have 12, so we can add 7 (at index 0) and 12 together to give us 19, so we are going to store 19 here.

@ index 3: we have 7, here we can add (7 + 12) which gives us the 19 which we have previously at index 2 in our maxSums array, or we can add (10 + 7) or even (7 + 7) and skip 10 and 12. So we choose to add (7 + 12) since it gives us 19 which is the greatest sum.

@ index 4: we have 9, here we can add (7 + 12 + 9) which gives us 28 which is the solution. but there are a bunch of other possibilities that will give us a smaller sum.

And as you can notice as we move to the right of the array, the amount of sums that we can generate grows and it becomes a lot more complicated to do this just by the head.

@ index 5: we have 14, here we can add (10 + 7 + 14) which gives us 31, and this is greater than 28, but it is not the solution. The solution is (7 + 12 +14) which gives us 33.

How do we find a formula for this, is there a pattern?

The answer is Yes.

Let's take the example of the 14 (at index 5) in our input array which we used to get 33. We actually have only 2 choices to generate 33: 1- Either to go to the max sum at the previous index (which is 28), and we know that the 28 could have the corresponding number at that index in the input array (which is 9) in it. So we can't add 14 to 28, so pick this 28 as our max sum.

2- Or we go one index further back and take 19 (@ index 3 in our maxSums array), we know that is 19 will not have the 9 (@ index 4 in the original array) because the 9 is one index ahead of it. So we can definitely add 14 to 19 and this does indeed give us the answer 33 😉

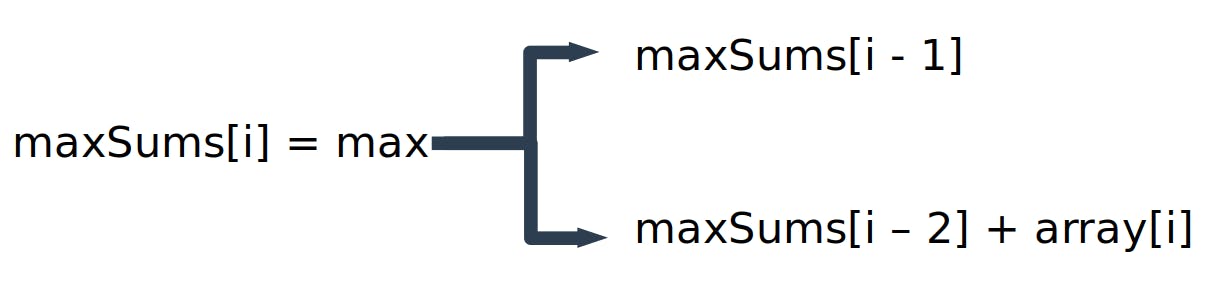
By looking at the formula we just came up with, we can see that we rely on maxSums[i - 1] and maxSums[i - 2]. So this tells us that we have 2 base cases that we need to generate. We need to generate maxSums[0] and maxSums[1] without being able to apply the formula.

maxSums[0] is just the first number in the input array and maxSums[1] is the greatest number between the first 2 numbers in the input array. Then the formula in action for the third element in maxSums array is: maxSums[2] = max( maxSums[1], maxSums[0] + array[2]) maxSums[2] = max(10, 7 + 12) ⇒ 19 and so on.

Time and Space Complexity Analysis:

Since we iterate through this array once, visiting every number, and at each element, we apply our formula which does a couple of basic comparison operations which run at constant time. Then our total time complexity is going to be O(N), where n is the size of our input array.
The space complexity is O(N) as well because we are building an array of length N.

Can we do better?

Yes we can 😉

We must at least visit each element once, so we can't lower our time complexity. But we can lower our space complexity.

If we look at our formula again, we only look at the last two elements of our maxSums array. So we only need two stored values at any given point in time, we don't need the entire array of length N.

We can have a variable called first to represent maxSums [i - 1] and second to represent maxSums[i - 2], and at the end of every iteration, we will have to update the first and second variables by there new values for the next iteration.

This will turn our space complexity to O(1) which is constant space. And, this is the most optimal solution to this problem. which is very elegant and very clean. 😉

Solution

#include <vector>
using namespace std;

// O(n) time | O(n) space
int maxSubsetSumNoAdjacent(vector<int> array) {
  // Write your code here.
      if (array.size() == 0) {
        return 0;
    } else if (array.size() == 1) {
        return array[0];
    }
    vector<int> maxSums = array;
    maxSums[1] = max(array[0], array[1]);
    for (int i = 2; i < array.size(); i++) {
        maxSums[i] = max(maxSums[i - 1], maxSums[i - 2] + array[i]);
    }
    return maxSums[array.size() - 1];
}

Optimal Solution

#include <vector>
using namespace std;

// O(n) time | O(1) space
int maxSubsetSumNoAdjacent(vector<int> array) {
  // Write your code here.
    if (array.size() == 0) {
        return 0;
    } else if (array.size() == 1) {
        return array[0];
    }
    int second = array[0];
    int first = max(array[0], array[1]);
    for(int i = 2; i < array.size(); i++) {
        int current = max(first, second + array[i]);
        second = first;
        first = current;
    }
    return first;
}

Muhammad Khaled's Blog