In this question, we are given 2 inputs; the first is an integer value which represents the target amount of money. The second input is an array representing the coin denominations that are at our disposal. And, we can use as many as we want from any value of coins.

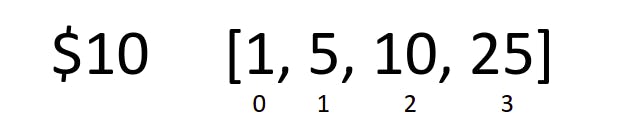
In this example, we have 4 ways to make the change for $10 using these coins:

1. use one $10 coin ⇒ 10 x 1
2. use two $5 coins ⇒ 5 x 2
3. use ten $1 coins ⇒ 1 x 10
4. use one $5 and five $1 ⇒ 5 x 1 + 1 x 5

To solve this, we are going to use dynamic programming:

Now, let's see the skeleton of the array that we are going to build to solve this problem 😉

We will construct a new array called ways, and each index of this array (and here I mean the number of the index itself) is going to represent a specific amount of money and it is going to go up to our target amount ($10 in our case).

So if our target amount is $100, then we will have a ways array of size 100 + 1, since we start from index 0.

• It is very important to start at zero dollars. Why? This is going to be clear in a second.

Every value we are going to store at each of these indices is going to represent the number of ways we have to make a change for the amount that is represented by the index (using the denominations only of course🙂).

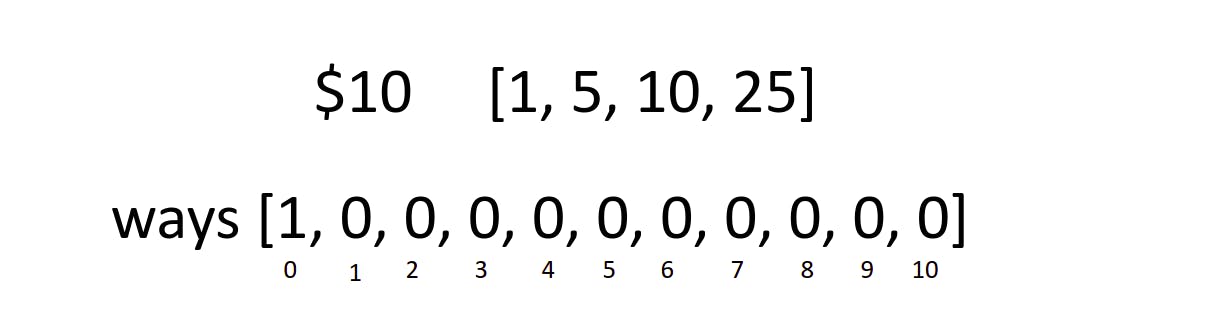
So we initialize the array all with zeros except at the first index, we have 1. Why?

This will serve our base case from an intuitive point of view. If we have a target amount of $0, there is just one way to make a change for zero dollars which is not to use any coins. And that is why we have 1 at our zero index.

Then we will iterate through all the denominations array starting from 1 in our case, and for each of the denominations, we are going to iterate through all the amounts in our ways array and update the number of ways there are to make a change for that amount.

Let's say we start with 1 in our denominations array. We go to our ways array at the index zero, and say is 1 (coin denomination) ≤ 0 (target amount) ? meaning: can we use a $1 coin to make $0? The answer is No, so we skip this point and move to the next index in our ways array.

And say, is 1 ≤ 1? The answer is Yes, so we are going to update our ways array using this formula: ways[1] += ways[1-1]

This means that ways[1] is going to be equal to whatever we have in ways[1] + ways[0],

But why ways[1 - 1]?

Because here we are saying what are the number of ways we have to make a change of (target amount - denomination amount) and we say add the number of these ways to the current number of ways we have stored at our current target value (which is one here). And this is going to give us the updated number of ways to make change for 1.

So here ways[1] += ways[1-1] ⇒ gives us 1. So we update our ways array to become:

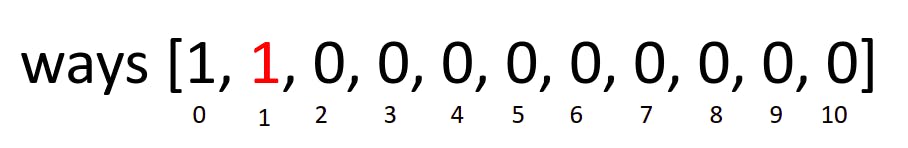
Then we move to the third index which is the amount of $2, and ask is 1 ≤ 2?

The answer is Yes, so we apply the same formula ways[2] += ways[2 - 1] which gives us 1. So we update our ways array to become:

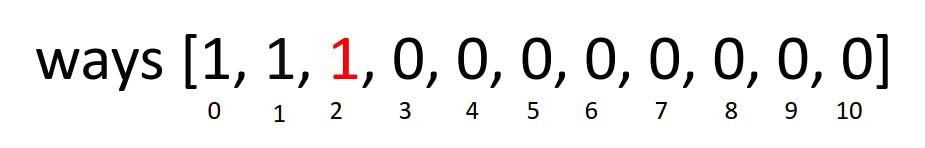
This means the number of ways to make a change of $2, given coins of value $1 is only one (which is using two $1 coins).

The rest of this iteration will follow in the same way resulting in updating the ways array to become:

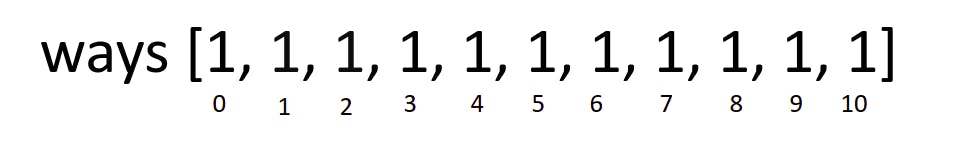
This makes sense from an intuition point of view, if we are only given $1 coins, for any amount, all we can do is to use whatever that amount is times $1 coins.

Now we move to the second denomination, which is 5. We say for each amount which is represented by the indices from 0 to 10) is 5 ≤ that amount? In other words, can we use a $5 denomination coin to generate that amount?

So we skip until we reach the first amount that is equal to 5:

Before we proceed further in updating the rest of the ways array, let's write the formula we use in a general way:

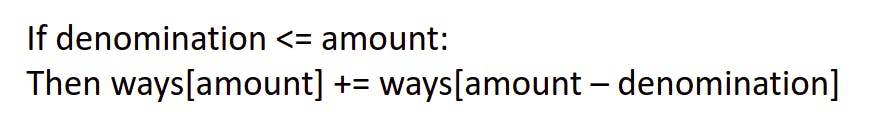
So after applying this formula to the rest of the ways array in this iteration, we get:

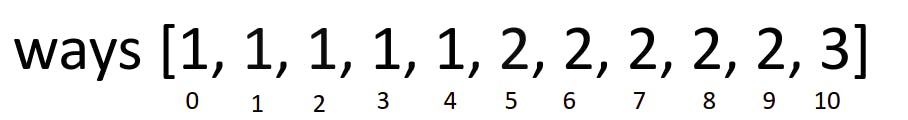
Then we get to our next denomination, which is 10. We say is 10 ≤ amount?

So we skip to the last element in the ways array, and update its value using our general formula:

And our ways array becomes:

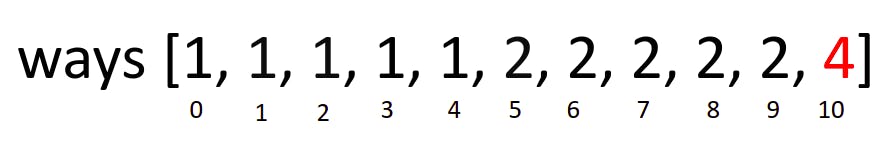
And since our last denomination is 25, which is greater than all of our amounts, we skip all of them and don't update the ways array anymore. We are never going to use a $25 coin to generate any of these amounts.

Space Time Complexity Analysis

• We are building an array of length N+1, where N is the target amount. So this converges to a space complexity of O(N).
• Time complexity is O(N x d), where d is the number of denominations. Because we are iterating through each of our denominations, and at each one of them, we iterate through an array of length (N+1). And for each of these iterations, we apply our formula which executes in constant time

Code Implementation

#include <vector>
using namespace std;

// O(nd) time | O(n) space
int numberOfWaysToMakeChange(int n, vector<int> denoms) {
    vector<int> ways(n + 1, 0);
    ways[0] = 1;
    for (int denom : denoms) {
        for (int amount = 0; amount < n + 1; amount++) {
            if (denom <= amount) {
                ways[amount] += ways[amount - denom];
            }    
        }
    }
    return ways[n];
}